| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 컴퓨터공학 #자료구조 #스택 #c++ #알고리즘 #백준문제풀이
- 컴퓨터공학 #c #c언어 #문자열입력
- 잔
- HTML #CSS
- 컴퓨터공학 #Java #자바 #클래스 #객체 #인스턴스
- BOJ #컴퓨터공학 #C++ #알고리즘 #자료구조
- Today
- Total
영벨롭 개발 일지
[자료구조] 연속된 자료 구조 VS 연결된 자료 구조 본문
프로그래머는 데이터를 메모리에 저장하기 위해 여러 자료 구조를 사용할 수 있습니다. 어떠한 자료 구조를 선택하느냐에 따라 시간 복잡도(time complexity)가 결정되는데, 이것은 특정 작업을 수행하는 데 걸리는 시간을 데이터 크기에 대한 수식으로 표현하는 방식입니다.
이러한 자료 구조는 크게 연속된 자료 구조와 연결된 자료 구조가 있습니다.
- 연속된 자료 구조(Array)
data_type arr[size];| index | 0 | 1 | 2 | 3 | ... |
| 원소 | data[0] | data[1] | data[2] | data[3] | ... |
- 대표적인 연속된 자료 구조에는 배열(array)가 있습니다.
배열은 메모리에 배열의 크기(size)보다 더 큰 공간이 있을 때 연속적으로 할당된 기억 공간입니다.
[ 배열의 특징 ]
1. index 기반의 자료구조
2. 연속적으로 할당된 기억 공간
3. 배열의 크기가 n이라면 n개의 자료를 하나의 주소( 0번째 index 주소)로 접근할 수 있음
[ 배열의 연산 ]
1. 검색(search)
배열에서 특정 원소를 검색하는 방법은 크게 두 가지가 있습니다.
(1) 선형 검색(linear search)
배열의 첫 번째 원소부터 차례대로 방문하면서 검색하고자 하는 원소와 동일한 원소가 있는지 확인하는 방법입니다.
최악의 경우 n개의 데이터를 모두 확인해야 하므로 시간 복잡도는 O(n)입니다.
(2) 이진 검색(binary search)
이진 검색은 선형 검색과 달리 정렬된 배열에서만 사용 가능합니다.
배열의 중간 원소를 중심으로 배열을 절반으로 분할하여 재귀적으로 탐색하는 방법입니다.
이때 시간 복잡도는 O(log n)으로 선형 검색보다 성능이 좋습니다.
2. 삽입(insert)
배열의 삽입 연산의 시간 복잡도는 O(n)입니다.
다음과 같은 배열 arr[5]에서 arr[2]에 문자 C를 삽입해봅시다.
| 0 | 1 | 2 | 3 | 4 | 5 |
| A | B | D | E |
먼저, 삽입하고자 하는 위치에 이미 데이터가 있음으로 arr[2]를 비워줘야겠죠?
arr[2]를 비우기 위해선 arr[2]와 arr[3]의 원소를 뒤로 한 칸씩 밀어줘야합니다.
차례대로 arr[4]에는 arr[3]의 원소를 저장, arr[3]에는 arr[2]의 원소를 저장하면 됩니다.
| 0 | 1 | 2 | 3 | 4 | 5 |
| A | B | D | E |
이제 arr[2]가 비었으니 문자 C를 삽입하면 됩니다!
| 0 | 1 | 2 | 3 | 4 | 5 |
| A | B | C | D | E |
3. 제거(delete)
배열의 제거 연산 또한 시간 복잡도는 O(n)입니다.
다음 배열에서 arr[2]의 원소를 제거해봅시다.
| 0 | 1 | 2 | 3 | 4 | 5 |
| A | B | D | E |
먼저, arr[2]에 있는 원소를 제거합니다. 간단하죠?
| 0 | 1 | 2 | 3 | 4 | 5 |
| A | B | E |
이제 arr[2]에 데이터가 비었으므로 빈공간이 생기지 않게 뒤에 있는 데이터를 앞으로 당겨주면 됩니다.
| 0 | 1 | 2 | 3 | 4 | 5 |
| A | B | E |
- 연결된 자료 구조(Linked list)
struct node{
data_type data;
node *link;
};
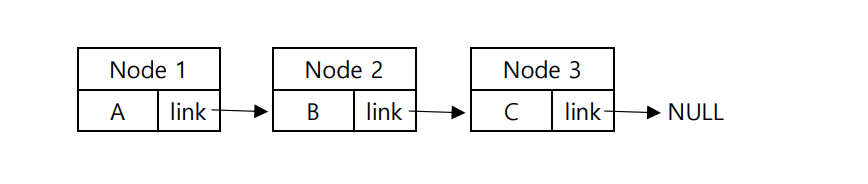
연결 리스트는 배열과 다르게 메모리에 연속된 공간을 요구하지 않습니다.
연결 리스트에서 각 원소는 노드라고도 불리는데, 메모리 공간의 임의의 위치에 저장되어 있으며 데이터와 링크를 가지고 있습니다. 각 노드는 다음 노드의 주소를 가리킵니다.
[ 연결 리스트의 특징 ]
1. 포인터 기반의 자료구조
2. 메모리 공간에 임의의 위치에 이산되어 저장되어 있음
3. 한 원소는 다음 원소를 가리키는 link를 가지고 있음
[ 연결 리스트의 연산 ]
연결 리스트는 배열과 다르게 원소를 순차적으로 접근해야만 합니다.
때문에 검색, 삽입 제거 연산의 시간 복잡도는 모두 O(n)이 됩니다.
1. 검색
선형 검색만 허용되기 때문에 head node부터 검색하고자 하는 원소와 동일한 원소를 찾을 때까지 다음 노드로 이동하며 탐색을 진행합니다.
2. 삽입
삽입 연산을할 때에는 삽입하고자 하는 위치 이전에 있는 원소의 link를 변경해주어야 합니다.
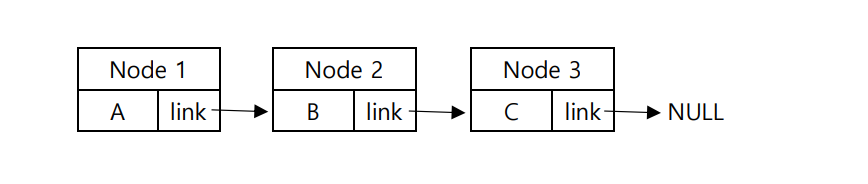
만약 위 그림에서 리스트의 순서를 A, D, B, C 로 하고 싶다면 먼저 Node 1번의 link를 NULL로 바꾸어 Node 1과 Node 2 사이의 연결을 취소해야합니다.
다음 새로운 노드를 Node 4번이라고 하겠습니다. Node 4번의 data는 'D', link는 NULL로 초기화 해줍니다.
이제 Node 1과 Node 4를 연결해야 겠죠? Node 1의 link가 Node 4를 가리키도록 합니다.
이제 Node 1과 Node 4는 연결이 되었습니다! 이제 Node 4의 link가 Node 2를 가리키도록 하면 삽입 연산이 완료 됩니다.
3. 제거
제거 연산도 마찬가지로 제거하고자 하는 위치 이전에 있는 원소의 link를 변경해주어야 합니다.
위 그림에서 Node 2를 제거하고 싶다면 Node 1의 link가 Node 3을 가리키도록 하면 됩니다.
즉, Node 2의 link를 Node 1의 link로 복사하면 됩니다. 간단하죠?
단, 연결 리스트에서 제거된 Node 2는 반드시 메모리 해제를(delete) 해주어야 합니다.
- 배열 vs 연결리스트
[ 특징 ]
| 배열 | 연결 리스트 | |
| 메모리 공간 | 연속된 기억 공간 | 이산된 기억 공간 |
| 공간 할당 | 정적/동적 할당 | 동적 할당 |
| 접근 경로 | 첫 번째 원소 주소 | 첫 번째 원소 주소 |
| 접근 방법 | index | pointer |
| 접근 방식 | Random access | Sequential access |
[ 연산 ]
| 배열 | 연결 리스트 | |
| 원소 접근 | O(1) | O(n) |
| 검색 | 선형 검색: O(n) 이진 검색: O(log n) |
O(n) |
| 삽입 | O(n) | O(n) |
| 삭제 | O(n) | O(n) |
'CS > 자료구조' 카테고리의 다른 글
| [자료구조]Hash 공부: 해싱, 충돌, 충돌 해결 (0) | 2022.03.30 |
|---|---|
| [자료구조]Graph 공부: 그래프의 종류, 인접행렬과 인접리스트 (0) | 2022.03.28 |
| [자료구조]Heap 공부: 최대 히입, 최소 히입 (0) | 2022.03.23 |
| [자료구조]Tree 공부: 이진트리 & BST & N항 트리 (0) | 2022.03.11 |




